[백준 알고리즘] 11659: 구간합 구하기4 (JAVA) 문제풀이

📌 [백준 알고리즘] 11659: 구간합 구하기4

👉백준 문제 바로가기

---

✅문제

수 N개가 주어졌을 때, i번째 수부터 j번째 수까지 합을 구하는 프로그램을 작성하시오.

---

✅입력

첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j가 주어진다.

---

✅출력

총 M개의 줄에 입력으로 주어진 i번째 수부터 j번째 수까지 합을 출력한다.’

---

✅제한

• 1 ≤ N ≤ 100,000
• 1 ≤ M ≤ 100,000
• 1 ≤ i ≤ j ≤ N

---

✅문제풀이

이 문제의 핵심은 시간복잡도를 고려애햐한다는 것이다. 문제의 시간 제한도를 확인한다면 “1초”라는 것을 확인할수 있다. 문제를 단순 for문을 사용하여 푼다면, 시간제한에 걸릴것이다 그렇기에 구간합이라는 알고리즘을 사용하고, 입력은 최악에 케이스를 고려해 가장큰 데이터가 들어올수 있음으로 scanner 보단 bufferedReader 사용한다.

---

구간합이란?? 합 배열을 이용하면서 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘이다.

• 합 배열 정의

S[i] = A[0] + A[1] + A[2] +…. + A[i-1] + A[i]
-> A[0]부터 A[i] 사이의 합을 구하기

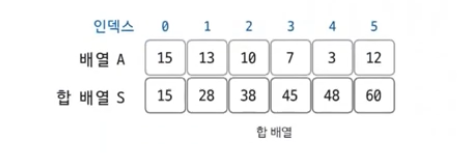
위에서 A[i]부터 A[j]까지의 배열 합을 합 배열 없이 구하는 경우, 최악의 경우는 i가 0이고 j가 N인 경우이므로 이떄 시간복잡도는 O(N) -> 하지만 합배열을 사용하면 O(1)안에 답을 구할 수 있음

• 합 배열을 만드는 공식 S[i] = S[i-1] + A[i]

• 구간 합을 구하는 공식 S[j] - S[i-1] -> i부터 j까지 구간의 합

이때 배열의 값이 자주 바뀐다면, 구간합 알고리즘이 아닌 세그먼트 트리의 개념을 사용하게 됨!

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Locale;
import java.util.StringTokenizer;

public class P11659_구간합구하기 {
    public static void main(String[] args) throws IOException {
        BufferedReader bufferedReader =
               new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stringTokenizer =
                new StringTokenizer(bufferedReader.readLine()); //토큰으로 값을 분리해서 사용

        int suNo = Integer.parseInt(stringTokenizer.nextToken()); //nextToken으로 String값을 받고 우리가 받아야하는 int향으로 형변환
        int quizNo = Integer.parseInt(stringTokenizer.nextToken());
        long[] S = new long[suNo + 1];  // 합배열 선언  0번쨰 인덱스를 무시하고 1번쨰 인덱스부터 데이터 입력
        stringTokenizer =
                new StringTokenizer(bufferedReader.readLine());
        
        
        for (int i = 1; i <= suNo; i++) {
            //입력 받은 수를 그대로 저장하는 것이 아닌 누적 합을 저장한다.
            S[i] = S[i - 1] + Integer.parseInt(stringTokenizer.nextToken());
        }//입력 끝


        for (int q = 0; q < quizNo; q++) {
            stringTokenizer =
                    new StringTokenizer(bufferedReader.readLine());
            int i = Integer.parseInt(stringTokenizer.nextToken());
            int j = Integer.parseInt(stringTokenizer.nextToken());
            System.out.println(S[j] - S[i-1]);
            //// 누적 합을 저장한 배열에서 i번 째 부터 j번 째 까지의 구간 합은 arr[j]에서 arr[i-1]을 뺀 것과 같다.
        }
    }
}